En 1915, dans le tumulte de la Première Guerre mondiale, la Cour de cassation de France rend une décision qui marquera profondément le droit de la propriété industrielle : l’arrêt Clément-Bayard. Ce jugement tire son nom de l’entreprise aéronautique impliquée dans l’affaire, et il deviendra une référence juridique incontournable. La raison de sa notoriété réside […]
Gerard Butler est un acteur emblématique de la trilogie « La chute » qui signifie en anglais « His fallen ». Il incarne dans les trois différents films d’action (la chute de la Maison-Blanche, de Londres puis du Président) le rôle de Mike Banning. L’acteur britannique n’est pas qu’un acteur de film d’action. Il joue également de nombreux autres […]

Comment démissionner de son poste en fast food ?
Le prénom Lucie, étincelant de grâce et chargé d’histoire, a traversé les siècles. Issu du latin ‘lux’, signifiant ‘lumière’, il évoque la clarté et la brillance. Cette racine le relie à l’image d’une personnalité rayonnante et éclatante. La popularité de Lucie a connu des fluctuations au gré des époques et des cultures, mais il a […]
La perte d’un portefeuille peut s’avérer être un moment particulièrement stressant, marqué par l’angoisse de l’inconnu et la crainte d’une utilisation frauduleuse de ses documents personnels. Pensez à agir promptement pour limiter les dégâts. Dès lors, plusieurs étapes doivent être entreprises sans délai : faire opposition sur les cartes bancaires, signaler la perte aux autorités […]
Vous aimerez partir vivre en Algérie ou alors y séjourner pour une certaine période et vous souhaiterez avoir une idée du coût de la vie ? En particulier vous voulez avoir des informations sur le salaire minimum qu’il faut pour vivre décemment dans ce pays d’Afrique du Nord. Comme partout ailleurs, cette information va dépendre de […]

Comment emprunter 180 000 euros sur 25 ans ?

IAD intranet : connexion au compte

Les critères à prendre en compte pour choisir son futur quartier

Les tendances actuelles du marché immobilier
Pour passer des moments de distraction, rien de mieux que de jouer avec sa console Nintendo Switch. En général, il arrive que des erreurs empêchent l’affichage de votre console sur une télé. Vous désirez connaître les raisons du problème de connexion TV de votre switch. Découvrez-les ici. Les raisons du problème de connexion TV de […]
L’univers passionnant de l’intelligence artificielle connaît actuellement une transformation sans précédent, portée par l’essor de Yiaho. Cette pépite française se distingue par son offre exceptionnelle d’IA en ligne, toutes gratuites et d’une facilité d’utilisation déconcertante. Explorez avec nous ce paysage innovant où Yiaho se positionne comme un acteur majeur, répondant à divers besoins grâce à […]
Découverte des capitales commençant par la lettre F : informations et faits intéressants
L’exploration des métropoles mondiales est un voyage fascinant à travers l’histoire, la culture et l’architecture. S’intéresser aux capitales dont les noms débutent par la lettre F nous amène à traverser différents continents et à dévoiler des caractéristiques uniques. De l’Europe avec ses villes chargées d’histoire à l’Afrique où les capitales bouillonnent d’une énergie sans pareil, […]
Les couvertines sont des éléments essentiels dans la réalisation d’une construction ou la rénovation d’un bâtiment, notamment en ce qui concerne la protection et l’esthétisme de celui-ci. Parmi les diverses options disponibles sur le marché, les couvertines aluminium connaissent un succès grandissant grâce à leurs nombreux atouts. Qu’est-ce que la couvertine alu ? La couvertine […]
L’intervention de divers professionnels est inévitable dans le cadre d’une rénovation de maison. L’un des plus importants est le plaquiste, un expert en pose de plaques de plâtre. Si vous envisagez une rénovation, l’embauche d’un plaquiste expert fera toute la différence dans vos finitions… L’importance d’un plaquiste dans un projet de rénovation Un plaquiste est […]

Le piercing au cartilage de l’oreille : pourquoi y penser ?

Les essentiels incontournables du dressing à ne pas négliger

Quel est votre morphotype ?

Comment taille la marque FIGL ?
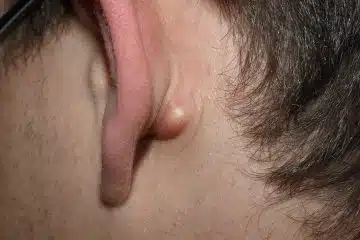
Le Kyste est une maladie qui se manifeste par une apparition de cavité contenant un liquide. L’une des zones du corps qu’attaque très souvent cette maladie est le lobe de l’oreille. Comment traiter le Kyste du lobe de l’oreille ? Si vous vous êtes déjà posés une fois cette question, vous êtes au bon endroit. Découvrez […]

Comment faire le bon choix de votre auto d’occasion ?

Quel véhicule choisir pour le camping : camping-car ou caravane ?

Tout savoir sur le choix d’une voiture Nissan pas cher